🔬 A Deep Dive into Vector Spaces: The Essence and Core Meaning of Eigenvalues, Eigenvectors, and the Eigendecomposition

At the heart of linear algebra lies a powerful set of concepts that not only unlock deep geometric insights but also form the mathematical backbone of modern data science, physics, and machine learning: eigenvalues, eigenvectors, and eigendecomposition.

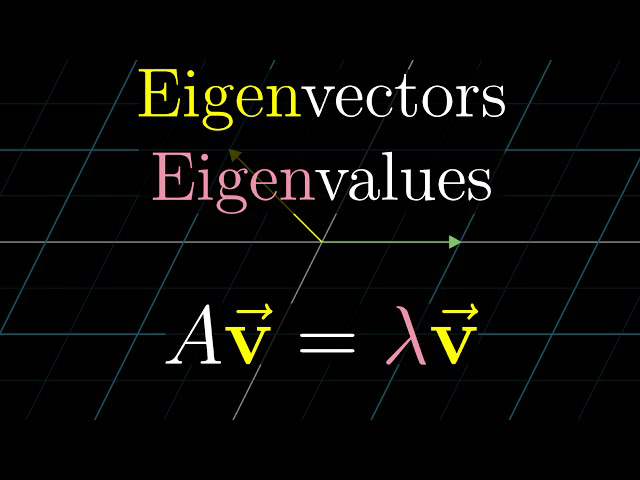
📐 What Are Eigenvectors and Eigenvalues?

In simple terms, an eigenvector of a square matrix is a non-zero vector whose direction remains unchanged when that matrix is applied to it. It may get stretched, compressed, or flipped, but it still points along the same line.

Mathematically, for a matrix A and a vector v, if:

A * v = λ * v

then:

• v is the eigenvector
• λ (lambda) is the eigenvalue corresponding to that eigenvector

🔄 Why Are They Important?

Eigenvectors and eigenvalues reveal the invariant properties of linear transformations. They help us understand how a transformation acts geometrically — which directions it stretches or compresses, and by how much.

This has wide-ranging applications:

• Principal Component Analysis (PCA) in machine learning
• Stability analysis in control theory and physics
• Graph analysis via spectral clustering
• Quantum mechanics to find stable states of systems

🧩 The Geometric Interpretation

Imagine a transformation like rotating, stretching, or squashing a vector space. Most vectors will change direction under this transformation. But a few special ones — the eigenvectors — stay aligned to their original direction. The eigenvalues tell you how much they’re scaled.

If an eigenvalue is:

• Greater than 1: the vector is stretched
• Between 0 and 1: the vector is compressed
• Negative: the vector flips direction
• Zero: the transformation collapses that direction completely

🧠 What Is Eigendecomposition?

Eigendecomposition is the process of breaking a matrix into its eigenvalues and eigenvectors — essentially exposing its core structure.

For a diagonalizable matrix A, it can be decomposed as:

A = V * D * V⁻¹

Where:

• V is a matrix whose columns are the eigenvectors of A
• D is a diagonal matrix with eigenvalues of A on the diagonal
• V⁻¹ is the inverse of V

This decomposition is like rewriting the transformation in its “native language”. Once in this form, it's easy to raise A to a power, simulate dynamics, or perform data compression.